Project Euler - Problem 607

Marsh Crossing

Problem 607

フロドとサムは、真東に向かって A 点から B 点に 100 リーグ移動する必要がある．通常の地形では、1 日に 10 リーグ踏破することができ、全体で 10 日かかる．しかし，その道は南西から北東へと正確に走る長い沼地が交差し，沼地を歩くと速度が減速する．沼地はすべての地点で幅 50 リーグであり，AB の中間点は沼地の中央に位置している．地域の地図を下に示す：



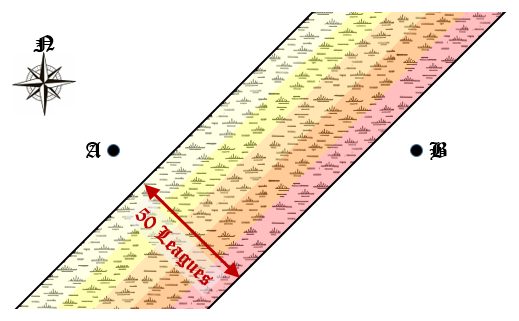
沼地は，地図の陰影に示すように 5 つの異なる領域から成る．ポイント A に最も近い領域は比較的軽い沼地であり，1 日あたり 9 リーグのスピードで移動することができる．しかし徐々に移動が難しくなり，ポイント B に近づくにつれ各領域での移動速度は 1 日あたり 8, 7, 6, そして最終的に 5 リーグになり，沼地を抜けると再び速度が 1 日あたり 10 リーグに戻る．

フロドとサムがポイント B へ向けて直線的に東へ向かうならば，彼らはちょうど 100 リーグを移動し，その旅は約 13.4738 日かかる．ただし，この時間は直線経路から逸脱すると短縮される．

ポイント A から B に移動するのに必要な最短移動時間を求め，小数点以下第 10 位を四捨五入して答えよ．

日本語訳がないのでグーグル先生に手伝ってもらうことになった

AB の中点を原点とし，直線 AB と x 軸が重なるように xy 直交座標系を定めると，各沼地の境界は

直線 $ \ell_k : y = x - 5 \sqrt{2} (2k - 5) \ (k = 0, 1, ..., 5) $

によって表される．

各直線 $ \ell_k $ 上に点 $P_k (x_k, y_k) $ を適当に配置する．

各境界上の点を通過するルートを考える ( A -> P₀ -> P₁ -> P₂ -> P₃ -> P₄ -> P₅ -> B )．

同一の地形で蛇行するのは明らかに時間の無駄なので，二点間は直線で結んでよい．

$ \mathrm{dist\lbrack\rbrack} = \{ \ AP_0 \ , P_0P_1 \ , P_1P_2 \ , P_3P_4 \ , P_4P_5 \ , P_5B \ \} $
$ \mathrm{v\lbrack\rbrack} = \{10, 9, 8, 7, 6, 5, 10\} $

とおくと，全体の所要時間 $T$ は，

$ \displaystyle T = \sum_{i = 0}^{5} \frac{ \mathrm{ dist\lbrack i \rbrack } }{ \mathrm{ v\lbrack i \rbrack } }$

と表せる．

$ x_k = y_k + 5 \sqrt{2} (2 k-5) $

であることを利用して書き下すと，

\begin{align*} \scriptsize{ T = \frac{1}{10} \sqrt{{y_0}^2+\left({y_0}-25 \sqrt{2}+50\right)^2}+ \frac{1}{9} \sqrt{({y_0}-{y_1})^2+\left(-{y_0}+{y_1}+10 \sqrt{2}\right)^2}+ \frac{1}{8} \sqrt{({y_1}-{y_2})^2+\left(-{y_1}+{y_2}+10 \sqrt{2}\right)^2}+ \\ \qquad \frac{1}{7} \sqrt{({y_2}-{y_3})^2+\left(-{y_2}+{y_3}+10 \sqrt{2}\right)^2}+ \frac{1}{6} \sqrt{({y_3}-{y_4})^2+\left(-{y_3}+{y_4}+10 \sqrt{2}\right)^2}+ \frac{1}{5} \sqrt{({y_4}-{y_5})^2+\left(-{y_4}+{y_5}+10 \sqrt{2}\right)^2}+ \frac{1}{10} \sqrt{{y_5}^2+\left({y_5}+25 \left(\sqrt{2}-2\right)\right)^2} } \end{align*}

各 y_k の関数になっていることがわかる．あとはこれを適当に動かして最小化する．

ここは Mathematica 先生にがんばってもらいます．

x[y_,k_]:=y+5Sqrt[2](2k-5);
y[i_]:=ToExpression["y"<>ToString[i]];
ys=Table[y[i],{i,0,5}];
P[i_]:={x[y[i],i],y[i]}
Distance[P_,Q_]:=Sqrt[(P[[1]]-Q[[1]])^2+(P[[2]]-Q[[2]])^2];
Distance[P_]:=Table[Distance[P[[i]],P[[i+1]]],{i,Length[P]-1}];
Ps={};
AppendTo[Ps,{-50,0}];
Do[AppendTo[Ps,P[i]],{i,0,5}];
AppendTo[Ps,{50,0}];
dist=Distance[Ps];
v={10,9,8,7,6,5,10};
T=Sum[dist[[i]]/v[[i]],{i,Length[dist]}];

こうして

ans=NMinimize[T,ys,PrecisionGoal->20,AccuracyGoal->20]

こう

ババーン

0.06 秒